Program Linear Dua Variabel | Matematika Kelas XI

Sahabat Latis, apa yang dimaksud dengan program linear dua variabel? Pada pembahasan kali ini, kita akan belajar tentang apa itu program linear dua variabel, menentukan daerah penyelesaian, persamaan garis, menentukan Sistem Pertidaksamaan Linear Dua Variabel (SPtLDV), nilai optimum, dan penyelesaian masalah dengan program linear.

Program Linear Dua Variabel

Program linear dua variabel (PtLDV) merupakan sebuah program matematika untuk menyelesaikan persoalan matematika di mana batasannya berbentuk sistem pertidaksamaan linear dua variabel.

Pada materi kali ini, Sahabat Latis akan mempelajari cara menggambar daerah penyelesaian dari pertidaksamaan linear dua variabel dan sistem pertidaksamaan linear dua variabel.

A. Menentukan Daerah Penyelesaian

Daerah penyelesaian adalah himpunan penyelesaian yang bernilai benar dari pertidaksamaan linear dua variabel (PtLDV) maupun sistem pertidaksamaan linear dua variabel (SPtLDV). Daerah penyelesaian tersebut dapat dibuktikan dengan pendekatan grafik pada bidang kartesius.

Bagaimana cara menentukan daerah penyelesaian? Berikut adalah langkah-langkahnya.

Menentukan dua titik sembarang dari soal pertidaksamaan.
Menarik garis lalu menghubungkan kedua titik yang membagi bidang kartesius.
Menguji nilai titik pada salah satu bagian dengan metode substitusi nilai x dan y titik pertidaksamaan.
Daerah penyelesaian selalu bernilai benar. Namun, penyelesaian berada di bidang lawan jika bernilai salah.
Pertidaksamaan memiliki sama dengan sebagai daerah penyelesaian.

B. Persamaan Garis dan Menentukan Sistem Pertidaksamaan Linear Dua Variabel (SPTLDV)

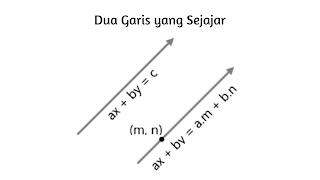
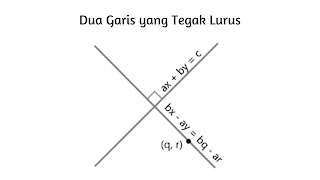
Persamaan garis dapat dibentuk dari garis yang terdapat di bidang kartesius. Garis-garis tersebut adalah garis yang melewati satu titik, garis yang memotong sumbu x dan y, garis yang melewati titik sembarang, dua garis yang sejajar, dan dua garis yang tegak lurus.

Garis yang Melewati Satu Titik

Source: amyarie

Bentuk umum: y-b=m(x-a)

Garis yang Memotong Sumbu X dan Y

Source: amyarie

Bentuk umum: bx+ay=ab

Garis yang Melewati Titik Sembarang

Source: amyarie

Bentuk umum: (y- y_1)/(y_2- y_1 )= (x- x_1)/(x_2- x_1 )

Dua Garis yang Sejajar

Source: amyarie

Dua Garis yang Tegak Lurus

Source: amyarie

Menentukan sistem pertidaksamaan linear dua variabel (sptldv) dapat diselesaikan dengan jumlah garis, rumus-rumus, dan uji nilai titik.

C. Nilai Optimum

Nilai optimum merupakan nilai minimum dan maksimum dari sasaran [f(x,y)] suatu wilayah penyelesaian pada program linear. Nilai optimum terletak pada pojok batas daerah penyelesaiannya.

Cara menentukan nilai optimum adalah dengan menerapkan metode uji titik pojok dan garis selidik.

Uji Titik Pojok

Uji titik pojok dapat dilakukan dengan mengikuti beberapa langkah berikut ini.

Buat gambar daerah penyelesaian jika belum ada.
Menentukan koordinat titik pojok masing-masing.
Memasukkan nilai x dan y ke rumus persamaan garis.

Garis Selidik

Ikuti langkah-langkah berikut untuk membuat garis selidik.

Menentukan skala garis selidik menggunakan sasaran atau fungsi objektif [f(x,y)= k].
Nilai optimum merupakan garis selidik yang tidak memotong daerah penyelesaian saat menyelidiki suatu titik pojok.
Jika nilai x positif, maka nilai maksimum berada di titik yang lebih kanan dan nilai minimum di titik yang lebih kiri.
Jika nilai x negatif, maka nilai maksimum berada di titik yang lebih kiri dan nilai minimum di titik yang lebih kanan.

Contoh Soal

Ditanya:

Pedagang buah memiliki modal Rp.1.000.000 untuk membeli apel dan pisang untuk dijual kembali. Harga beli tiap kilogram apel Rp.4.000 dan pisang Rp.1.600. Tempatnya hanya bisa menampung 400 kilogram buah. Tentukan jumlah apel dan pisang agar kapasitas maksimum!

Dijawab:

Mari kita jawab soal ini dengan membuat model matematikanya.

Misalnya apel adalah x dan pisang adalah y.

x +y ≤ 400 → Kapasitas tempat

4.000x + 1.600y ≤ 1.000.000

5x + 2y ≤ 1.250 → Modal

x ≥ 0

y ≥ 0

Setelah itu, mari kita menggambar daerah penyelesaiannya.

Titik ekstrim:

A (0,400) bukan optimum karena tidak ada apel

C (250,0) bukan optimum karena tidak ada pisang

B (X_B,Y_B)

(5x+2y ≤1250)-(2x+2y ≤800)=3x ≤450

⟺3x≤ 450

⟺ x≤ 150

⟺ y≤ 250

Sehingga jumlah maksimumnya adalah:

Apel: 150 kg

Pisang: 250 kg

Menyelesaikan Masalah dengan Program Linear

Bagaimana cara menyelesaikan masalah dengan program linear? Terdapat tiga metode untuk menjawab tantangan tersebut yaitu:

Soal cerita dengan dua variabel
Soal cerita yang diubah dalam bentuk pertidaksamaan
Pertidaksamaan dalam bentuk harga

Untuk memahami lebih jauh tentang cara menyelesaikan masalah matematika menggunakan program linear, mari mempelajari contoh soal berikut ini.

Contoh Soal

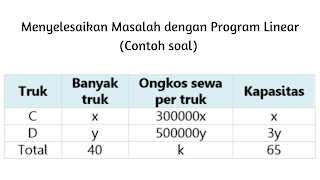
Perusahaan air minum akan mengangkut galon air seberat 65 ton dari Malang ke Bandung menggunakan dua jenis truk. Truk C berkapasitas 1 ton dengan harga sewa Rp.300.000. sedangkan truk D berkapasitas 3 ton dengan harga sewa Rp.500.000. Jika perusahaan tersebut harus menyewa setidaknya 40 truk dari kedua truk, tentukan:

Banyak masing-masing truk agar biaya pengangkutan sekecil mungkin.
Biaya pengangkutan yang paling murah.

Dijawab:

Source: amyarie

Maka model matematika yang dapat dibuat adalah sebagai berikut.

x ≥0,x є C

y ≥0,x є C

x+ y ≥40

x+ 3y ≥65

300000x+500000y=k (fungsi sasaran)

Titik potong:

(x+3y=65)-(x+y=40)=2y=25

⟺ y≤ 12,5

⟺ x≤ 27,5

Karena x dan y bukan merupakan bilangan cacah, maka titik di sekitar titik potong lah yang merupakan nilai minimum (biaya terkecil).

Uji nilai titik di sekitar titik potong dengan pertidaksamaan 3 dan 4:

Titik (27, 12): (27) + (12) ≥ 40 (salah)
Titik (28, 12): (28) + (12) ≥ 40 (benar), (28) + 3(12) ≥ 65 (salah)
Titik (27, 13): (27) + (13) ≥ 40 (benar), (27) + 3(13) ≥ 65 (benar)
Titik (28, 13): (28) + (13) ≥ 40 (benar), (28) + 3(13) ≥ 65 (benar)

Nilai terendah dan benar dari uji titik di sekitar titik potong adalah titik (27, 13).

Jadi, jumlah truk C ada 27 truk dan jumlah truk D ada 13 truk. Maka biaya terkecil yang dapat digunakan adalah: 300000(27) + 500000(13) = Rp14.600.000.