Pertidaksamaan Linear Dua Variabel | Matematika Kelas XI

Sahabat Latis, kali ini kita akan membahas tentang pertidaksamaan linear dua variabel (PtLDV). Dalam hal ini, kita diminta untuk menentukan nilai minimum dan maksimum, serta penyelesaian kontekstual yang terkait dengan pertidaksamaan linear dua variabel.

Pertidaksamaan Linear Dua Variabel

Apa yang akan kita pelajari pada materi kali ini?

Terdapat beberapa hal yang harus Sahabat Latis ketahui tentang pertidaksamaan linear dua variabel.

Di antaranya adalah mengetahui pengertian pertidaksamaan linear dua variabel, menyusun pertidaksamaan linear dua variabel ke daerah penyelesaiannya, metode penyelasaian pertidaksamaan linear dua variabel, dan membuat model matematika berdasarkan permasalahannya.

A. Apa Itu Pertidaksamaan Linear Dua Variabel?

Pertidaksamaan (<, >, ≤, ≥)adalah kalimat terbuka yang memiliki bentuk seperti:

ax+by (R) c

Keterangan:

a, b, dan c adalah konstanta

x dan y merupakan variabel

R merupakan perwakilan dari pertidaksamaan (< ,>,≤,≥)

Grafik pertidaksamaan linear dua variabel (PtLDV) merupakan himpunan semua titik x,y pada sistem koordinat Cartesius yang memenuhi PtLDV.

Himpunan penyelesaian pada grafik PtLDV digambarkan sebagai daerah yang diarsir.

Menentukan Persamaan Garis

Terdapat beberapa cara untuk menentukan persamaan garis yaitu persamaan segmen garis, persamaan garis melalui titik 〖(x〗_1,y_1) dengan gradien m, dan persamaan garis melalui titik 〖(x〗_1,y_1) dan 〖(x〗_2,y_2).

Persamaan Segmen Garis

Source: amyarie

Persamaan garis yang melalui titik (a,0) dan (0,b) adalah x/a + y/b=1 atau bx+ay=ab.

Persamaan Garis melalui Titik 〖(x〗_1,y_1) dengan Gradien m

Persamaan garis yang melalui titik 〖(x〗_1,y_1) dan gradien m adalah y- y_1=m(〖x- x〗_1 ).

Persamaan Garis melalui Titik 〖(x〗_1,y_1) dan 〖(x〗_2,y_2)

Persamaan Garis melalui Titik 〖(x〗_1,y_1) dan 〖(x〗_2,y_2) adalah x/x_2 + x_1/x_1 = y/y_2 + y_1/y_1 atau y- y_1=〖y_2 - y〗_1/〖x_2 - x〗_1 (〖x- x〗_1 ), dengan x_1 ≠ x_2.

Menentukan Titik Koordinat

Jika titik koordinat mudah diukur, maka:

Jika y = 0 yang memotong sumbu x pada grafik bx+ay=ab, maka bx+a×0=ab ⟺x=a. Koordinat titik potong grafik tersebut dengan sumbu x adalah (a,0).
Jika x = 0 yang memotong sumbu x pada grafik bx+ay=ab, maka bx+a×0=ab ⟺x=a. Koordinat titik potong grafik tersebut dengan sumbu y adalah (0,b).

B. Metode Penyelesaian Pertidaksamaan Linear Dua Variabel

Terdapat dua cara menyelesaikan pertidaksamaan linear dua variabel. Di antaranya adalah metode substitusi dan metode koefisien y.

1. Metode Substitusi

Metode substitusi merupakan metode yang digunakan untuk mengganti titik 〖(x〗_1,y_1) yang berada di luar garis bx+ay=ab.

Himpunan penyelesaiannya adalah daerah yang memuat titik 〖(x〗_1,y_1) jika 〖bx〗_1+ 〖ay〗_1-ab >0. Sedangkan daerah yang memuat titik 〖(x〗_1,y_1) apabila 〖bx〗_1+ 〖ay〗_1-ab <0 bukanlah himpunan penyelesainnya.

2. Metode Koefisien y

Himpunan penyelesaian menggunakan metode koefisien y dapat dilihat dari nilai a yang lebih besar atau lebih kecil dari 0 (nol) dengan pertidaksamaan sbb.

Source: amyarie

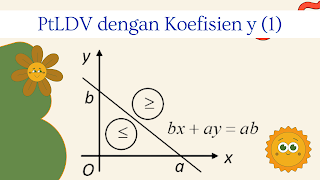
Apabila a>0 dimana bx+ay≥ab maka himpunan penyelesaiannya berada di atas garis bx+ay=ab.

Source: amyarie

Apabila a>0 dimana bx+ay≤ab, maka himpunan penyelesainnya berada di bawah garis bx+ay=ab.

Source: amyarie

Apabila a<0 dimana bx+ay≥ab, maka himpunan penyelesainnya berada di bawah garis bx+ay=ab.

Source: amyarie

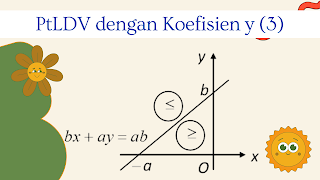
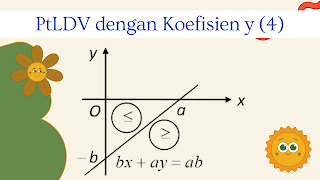
Apabila a<0 dimana bx+ay≤ab, maka himpunan penyelesainnya berada di atas garis bx+ay=ab.

Contoh Soal

Agar lebih memahami metode yang digunakan untuk memecahkan persoalan pertidaksamaan linear dua variabel, pelajari contoh soal berikut ini.

Ditanya:

Tentukan daerah himpunan penyelesaian yang memenuhi pertidaksamaan dari x+2y≤4!

Dijawab:

x+2y≤4 ⟹ persamaan garisnya adalah x+2y≤4

y=0 →x+2 ×0=4⟺x=4⟹(4,0)

y=0 →0+2y=4⟺y=2⟹(0,2)

Sehingga, didapatlah titik potong garis x+2y≤4 dengan sumbu x dan y masing-masing adalah (4,0) dan (0,2).

Karena koefisien y di sini x+2y≤4 bernilai positif, maka himpunan penyelesaiannya berada di bawah garis x+2y≤4.

Source: amyarie

C. Langkah-langkah Penyelesaian dan Contoh Soal

Bagaimana cara menyelesaikan sistem pertidaksamaan linear dua variabel? Ketika Sahabat Latis diminta untuk menyelesaikan soal pertidaksamaan linear dua variabel, kalian dapat mengikuti langkah-langkah berikut ini.

Menyatakan pertidaksamaan linear ke persamaan linear dalam bentuk ax+by= c.
Menentukan titik potong garis ax+by=c, x dan y adalah sumbunya.
Menentukan garis lurus yang menghubungkan dua titik potong. Garis dilukis tidak putus-putus apabila pertidaksamaan dihubungkan dengan tanda ≤ atau ≥. Jika pertidaksamaan tersebut dihubungkan dengan tanda < atau > maka garis dilukis secara putus-putus.
Menentukan sebarang titik (x,y) lalu memasukkannya ke dalam sebuah pertidaksamaan. Daerah penyelesaian selalu bernilai benar dan berlaku sebaliknya.
Mengarsir daerah yang penuh karena merupakan himpunan penyelesaian.

Contoh Soal

Untuk lebih jelasnya, mari kita pelajari contoh soal berikut ini.

Ditanya:

Tentukan himpunan penyelesaian pertidaksamaan linear dari 3x+2y≥12!

Dijawab:

Langkah 1:

Tentukan garis pembatas yaitu 3x + 2y = 12.

Langkah 2:

Tentukan titik potong terhadap sumbu X dan sumbu Y.

Titik potong sumbu X adalah jika y = 0.

Sehingga diperoleh:

3x + 2(0) = 12

⇔ 3x + 0 = 12

⇔ 3x = 12

⇔ x = 4

Jadi, titik potong terhadap sumbu X adalah (4,0).

Titik potong sumbu Y adalah jika x = 0.

Sehingga diperoleh:

3(0) + 2y = 12

⇔ 0 + 2y = 12

⇔ 2y = 12

⇔ y = 6

Jadi, titik potong terhadap sumbu Y adalah (0,6).

Langkah (3):

Menghubungkan kedua titik potong tersebut dengan garis lurus.

Langkah (4):

Mengambil sembarang titik, misalnya (0, 0), lalu masukkan ke pertidaksamaan:

3(0) + 2(0) ≥ 12 (tidak memenuhi), berarti daerah tempat titik (0, 0) bukanlah merupakan daerah himpunan penyelesaian.

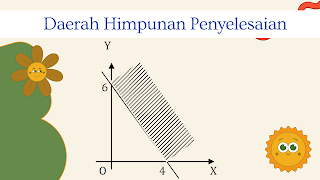
Langkah (5):

Mengarsir daerah yang memenuhi.

Keynote:

Tanda pertidaksamaan ≥ mengisyaratkan daerah penyelesaian yang berada di sebelah kanan atas garis.
Tanda pertidaksamaan ≤ mengisyaratkan daerah penyelesaian yang berada di sebelah kiri bawah garis.