Logika Matematika | Matematika Kelas XI

 

Sahabat Latis, apa yang dimaksud dengan logika matematika?

Ketika kita menghadapi suatu masalah, kita akan membahas masalah tersebut dan mencari jalan keluarnya berdasarkan logika atau pemahaman kita.

Pertama, pahami terlebih dahulu pernyataannya. Setelah itu, barulah kita menentukan nilai kebenaran dari pernyataan yang ada. 

Ketika semua kebenaran telah terungkap, saatnya bagi Sahabat Latis untuk merumuskan pernyataan. Sehingga, nantinya kita mendapatkan kesimpulan yang tepat.

Logika Matematika

Pada materi kali ini, Sahabat Latis akan mempelajari segala hal tentang logika matematika.

Mulai dari pernyataan, pernyataan majemuk, pernyataan majemuk bersusun, konversi, inversi, kontraposisi, pernyataan berkuantor, dan penarikan kesimpulan.

A. Kalimat Terbuka dan Pernyataan

Hal pertama yang mesti diketahui tentang logika matematika adalah kalimat terbuka dan tertutup.

Kalimat Terbuka

Kalimat terbuka merupakan kalimat yang tidak pasti nilai kebenarannya.

E.g.

Biarkan dia menemuinya!

Kapan kau pergi?

Pernyataan (Proposisi)

Pernyataan atau proposisi merupakan kalimat tertutup yang memiliki nilai benar atau salah terhadap suatu persoalan.

Pernyataan dilambangkan dengan huruf kecil seperti p, q, r, dan seterusnya. Sedangkan nilai kebenaran dilambangkan dengan τ(x), di mana S = salah dan B = benar.

E.g.

P: Hasil kali 4 dengan 5 adalah 20. [τ(p) = B]

Q: Seluruh bilangan prima bukanlah bilangan genap. [τ(q) = S]

B. Pernyataan Majemuk

Pernyataan majemuk merupakan dua pernyataan atau lebih yang dihubungkan dengan operasi logika matematika.

Operasi logika matematika yaitu konjungsi (Λ), disjungsi (V), implikasi (→), dan biimplikasi (↔).

Di akhir penyelesaian, nilai kebenaran ditulis dalam sebuah tabel kebenaran.

Konjungsi (Λ)

Konjungsi merupakan gabungan dua pernyataan tunggal dengan penghubung “dan”. Jika P dan Q mewakili masing-masing pernyataan, maka konjungsi tersebut ditulis dengan P∧Q.

Apabila kedua pernyataan tersebut bernilai benar, maka hasil konjungsinya adalah benar.

Disjungsi (V)

Disjungsi merupakan gabungan dari dua buah pernyataan dengan kata penghubung “atau”. Jika P dan Q mewakili masing-masing pernyataan, maka disjungsi tersebut ditulis dengan P∨Q.

Dalam kehidupan sehari-hari, kata “atau” bermakna salah satu atau keduanya. Namun, itu dapat diartikan dengan tidak keduanya. Sehingga, muncullah dua jenis disjungsi yaitu disjungsi inklusif dan disjungsi ekslusif.

Disjungsi Inklusif

Pernyataan logika dikatakan sebagai disjungsi inklusif apabila dua pernyataan bernilai benar. Sehingga ditulis dengan P∨Q.

Disjungsi Ekslusif

Pernyataan logika dikatakan sebagai disjungsi ekslusif apabila dua pernyataan bernilai benar jika salah satu dari pernyataan pernyataan dianggap benar. Sehingga ditulis dengan P∨/Q.

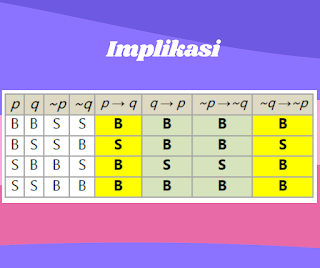
Implikasi (→)

Implikasi merupakan gabungan dari dua pernyataan P dan Q yang menggunakan kata penghubung “Jika..., maka...”. Kedua pernyataan tersebut dihubungkan dengan tanda panah P→Q.

Dalam hal ini, pernyataan P disebut dengan hipotesis atau anteseden. Sedangkan pernyataan Q disebut dengan kesimpulan atau konsekuen.

Jika hipotesis bernilai benar, namun kesimpulannya salah, maka P→Q hasilnya salah. Selain itu, pernyataan dianggap benar.

Implikasi terbagi atas konvers, invers, dan kontraposisi.

• Konvers merupakan kebalikan dari bentuk umum implikasi P→Q menjadi Q→P.
• Invers merupakan negasi dari pernyataan utama di mana P→Q menjadi ~P→~Q
• Kontraposisi merupakan kebalikan dari bentuk umum implikasi yang dinegasikan P→Q menjadi ~Q→~P

Biimplikasi (↔)

Biimplikasi atau bikondisional merupakan suatu pernyataan majemuk yang berbentuk ”P jika dan hanya jika Q”. Itu berarti “jika p maka q dan jika q maka p”. Pernyataan “p jika dan hanya jika q” dilambangkan dengan P↔Q.

Pernyataan biimplikasi P↔Q bernilai benar apabila P dan Q memiliki nilai kebenaran yang sama (semua benar atau semua salah). 

Namun jika nilai kebenaran P dan Q tidak sama, maka P↔Q merupakan pernyataan yang salah.

C. Ekuivalensi

Ekuivalensi dari dua pernyataan majemuk dapat dijawab menggunakan aljabar logika matematika dan tabel kebenaran yang dilambangkan dengan ≡.

Jenis-jenis sifat operasi logika matematika (aljabar) yaitu idempotent, involusi, komplemen, identitas, komutatif, asosiatif, distributif, de morgan, dan implikasi.

Idempoten

Involusi

Komplemen

Identitas

Komutatif

Asosiatif

Distributif

De Morgan

Implikasi

Sedangkan jenis-jenis tabel kebenaran dapat dilihat dari hasil akhir nilai kebenarannya yaitu tautologi, kontradiksi, dan kontingensi.

• Tautologi: kesimpulan yang bernilai benar secara keseluruhan.
• Kontradiksi: kesimpulan yang bernilai salah secara keseluruhan.
• Kontingensi: kesimpulan yang bernilai salah dan benar.

D. Penarikan Kesimpulan

Kesimpulan bernilai logis apabila nilai akhirnya bersifat tautologi A∧B →C. Terdapat tiga rumus logis premis yaitu modus ponen, modus tollen, dan silogisme.

Modus Ponen

Di mana premis satu adalah implikasi (P→Q) dan premis dua adalah Q. Sehingga menghasilkan Q (∴Q).

Modus Tollen

Di mana premis satu adalah implikasi (P→Q) dan premis kedua merupakan negasi Q (~Q). Sehingga menghasilkan negasi P (~P).

Silogisme

Di mana premis satu adalah implikasi (P→Q) dan premis kedua merupakan implikasi dari pernyataan lain (Q→R). Sehingga menghasilkan Jika P maka R (P→R).

Contoh Soal

Jika Andi bersahabat dengan Beni, maka Andi tidak bersahabat dengan Cindy. Cindy bersahabat dengan Desi atau Cindy tidak bersahabat dengan Andi. Jika Andi bersahabat dengan Desi, maka Cindy tidak bersahabat dengan Desi. Diketahui bahwa Andi berteman dengan Desi. (Andi, Beni, Cindy, dan Desi berturut-turut A,B,C, dan D).

Pembahasan:

Analogi:

P = “Andi berteman dengan Beni”

Q = “Andi berteman dengan Cindy”

R = “Cindy berteman dengan Desi”

S = “Andi berteman dengan Desi”

Pernyataan:

1.  P → ~Q
2.  R V Q ≡ ~R → Q
3.  S → ~R
4.  S

Kesimpulan:

Jadi, kesimpulannya adalah, Andi tidak berteman dengan Beni.

Baca juga: bimbel-cpns.id

Gimana Sahabat Latis, udah mulai paham kan dengan materi Logika Matematika?

Supaya kamu makin paham dengan materi lainnya, bisa jawab PR dan tugas di sekolah dengan mudah dan prestasi kamu meningkat tajam, kamu bisa coba ikutan les privat Latisprivat lho!

Gurunya berprestasi dan biayanya juga hemat. Bisa online dan tatap muka juga. Fleksibel kan? Untuk info lebih lanjut, kamu bisa hubungi Latisprivat di line chat 085810779967.

Sampai ketemu di kelas!

Referensi:

materi78.co.nr